Brownian Motion

[J_B_]

Brownian motion can never be in a straight line and is modelled by the Langevin equation.

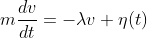
The first term in the right hand side of the equation is the resistance of a particle of mass m to the molecules in the medium and is proportional to the velocity of the particle v.
The proportionality constant λ is a damping coefficient.
The second term based on statistical mechanics is referred to as the noise term and represents the collisions of the air or liquid molecules with the particle.
The kinetic energy of the colliding molecules has a Gaussian distribution.

For motion to be in a straight line the general equation is;

where α is a constant.

Consider the case when there are no collisions on the particle (the second term is zero) and the force acting on the particle is purely resistance.
Solving the equation gives;

v₀ is the initial velocity and is clearly not a straight line.
One doesn’t even have to consider the noise term;

to show that straight line motion is impossible.

I'd love it if this could be established for a real world case, but your noise term is synthetic. I could pick anything, white noise, pink noise, etc. I'd be more interested in knowing if this holds when real forces are considered.

 

[sjastro]

I'd love it if this could be established for a real world case, but your noise term is synthetic. I could pick anything, white noise, pink noise, etc. I'd be more interested in knowing if this holds when real forces are considered.

What do you think statistical mechanics is based on?

 

[Bradskii]

OK. So is it A, B, ... or are you describing a 3rd option C?

All directions are equally likely.

 

[J_B_]

What do you think statistical mechanics is based on?

I'm not being snarky. I think your reply was very helpful; the equation was in terms I'm familiar with. As an engineer, I'd be happy to plug in some Gaussian noise, maybe run a test to get the statistical properties of the noise, and move on.

But @essentialsaltes has (intentional or not) challenged all that by digging deeper to express the actual inter-molecular forces rather than representing them with a statistical distribution. So ... do you expect the nonlinear result would hold generally, or does it need to be analyzed case by case?

I did some searching, and didn't find any cases where people were looking at straight line motion. There were cases about how many times the motion crosses a straight line, or how completely the motion fills a disc (fractal studies). Then there was also a long list of people claiming this system and that (chemical, electrical, mechanical, etc.) exhibited Brownian motion, but that doesn't explicitly answer my question.

 

[sjastro]

I'm not being snarky. I think your reply was very helpful; the equation was in terms I'm familiar with. As an engineer, I'd be happy to plug in some Gaussian noise, maybe run a test to get the statistical properties of the noise, and move on.

But @essentialsaltes has (intentional or not) challenged all that by digging deeper to express the actual inter-molecular forces rather than representing them with a statistical distribution. So ... do you expect the nonlinear result would hold generally, or does it need to be analyzed case by case?

I did some searching, and didn't find any cases where people were looking at straight line motion. There were cases about how many times the motion crosses a straight line, or how completely the motion fills a disc (fractal studies). Then there was also a long list of people claiming this system and that (chemical, electrical, mechanical, etc.) exhibited Brownian motion, but that doesn't explicitly answer my question.

I have altered my original post as zero collisions doesn't equate to motion not occurring in a straight line but this is beside the point.
Brownian motion is an example of entropic forces at work; forces that increase the entropy of the system.
A wind blows down a sandcastle into a random heap results in an increase in entropy.
One would not expect another strong wind to restore this heap to the original sandcastle; it is statistically highly improbable if not impossible.
The same principle applies to random collisions imparting straight line motion on a particle.

 

[J_B_]

I have altered my original post as zero collisions doesn't equate to motion not occurring in a straight line but this is beside the point.
Brownian motion is an example of entropic forces at work; forces that increase the entropy of the system.
A wind blows down a sandcastle into a random heap results in an increase in entropy.
One would not expect another strong wind to restore this heap to the original sandcastle; it is statistically highly improbable if not impossible.
The same principle applies to random collisions imparting straight line motion on a particle.

Ah! Excellent! It clicked for me with that last sentence. But let me try stating it a different way, and see if you still agree.

Newton's first law stipulates that a body with no forces acting upon it will move at constant velocity (including zero) in a straight line. Therefore, any force not aligned with the direction of motion will cause a deviation from the straight line. We don't need to invoke randomness. It is simply impossible that every force the particle will encounter will be aligned with the current direction of motion.

How does that sound?

 

[Bradskii]

If I was playing a dice game; and I rolled straight sixes, 100 times in a row; my opponents would suspect something other than random chance.

That's because sixes are recognised as 'a win'. Select any pair of numbers and write it down. Do the same again until you have 100 pairs. The chance of you rolling that sequence is exactly the same as rolling straight sixes 100 times.

 

[HARK!]

There were cases about how many times the motion crosses a straight line,

Was this real, and observable? If it follows a straight line for any distance that is measurable; then what would prohibit this from continuing, in sequence, until the particle reached the face of a cube?

 

[J_B_]

Was this real, and observable? If it follows a straight line for any distance that is measurable; then what would prohibit this from continuing, in sequence, until the particle reached the face of a cube?

Since it wasn't what I was looking for, I didn't dig into it.

 

[HARK!]

That's because sixes are recognised as 'a win'. Select any pair of numbers and write it down. Do the same again until you have 100 pairs. The chance of you rolling that sequence is exactly the same as rolling straight sixes 100 times.

I'm well aware of this. It is one of the pillars of my argument.

 

[Bradskii]

I'm well aware of this. It is one of the pillars of my argument.

But it's astonishing that so many people have a blank spot when it comes to statistics. If you asked people which sequence was more likely if you throw a die six times...

1 3 1 6 5 2
6 6 6 6 6 6

...it's amazing how many people pick the sixes (I just asked my wife, who is a very smart woman, and she picked them).

 

[essentialsaltes]

I may have muddled the question the first time, but I tried to clarify it to indicate a particular state.

Pick a starting point and an ending point. We know the state of the particle at the starting point. Is the state of the particle the same for every path when it reaches the ending point?

For the sake of simplicity, let's say the particle is not moving at the end. Then yes, because state variables only describe the state a particle (or system) is in at a moment. They do not carry their 'histories' with them.

 

[sjastro]

Ah! Excellent! It clicked for me with that last sentence. But let me try stating it a different way, and see if you still agree.

Newton's first law stipulates that a body with no forces acting upon it will move at constant velocity (including zero) in a straight line. Therefore, any force not aligned with the direction of motion will cause a deviation from the straight line. We don't need to invoke randomness. It is simply impossible that every force the particle will encounter will be aligned with the current direction of motion.

How does that sound?

To be exact the sum of all the forces acting on the body must equal zero which highlights the problem.
Since a force is imparted through the work-energy equation when a molecule collides with the body there must be another collision of equal magnitude in the opposite direction for the forces to cancel other each other out.
The kinetic energy of a molecule striking the body is random and to have these all the forces cancel each other out not only at some instant time t but also over the entire time the body travels in a straight line is highly unlikely to put it mildly.

Even allowing acceleration in a straight line requires the lateral collision forces to cancel each other out which is also statistically highly improbable.

 

[Tanj]

It's doesn't have to be ions, which being charged have other forces to contend with. Bacteria are subject to brownian motion, though good luck on getting them to the other side of the cube.

Clip D30_29_487, from Dissolve

 

[HARK!]

But it's astonishing that so many people have a blank spot when it comes to statistics. If you asked people which sequence was more likely if you throw a die six times...

1 3 1 6 5 2
6 6 6 6 6 6

...it's amazing how many people pick the sixes (I just asked my wife, who is a very smart woman, and she picked them).

However, in the REAL world, no die is perfectly weighted. Therefore the die will favor one side over the others. The mother of one of my customers owned an antique store for most of her life. She has numerous collections. After her mother passed, she gave me some of her mother's belongings. One of them is a large glass jar full of dice (about a gallon). At a glance, they all seem to have divots drilled out for the dots. The side with one dot retains most of the material in that side. The opposing side has six divots. More material has been removed from that side, than any other side. This means that the heaviest side of the die is opposite of the lightest side of the die. It would stand to reason that sixes would come up more often than ones. It would also stand to reason that straight sixes would come up more often than any other sequence.

Perhaps your wife is correct when it comes to the REAL world.

Now, lets apply this principle to a particle suspended in liquid. Based on it's imperfect shape, it would stand to reason that it would favor a motion in one direction, over all others.

 

[Tinker Grey]

However, in the REAL world, no die is perfectly weighted. Therefore the die will favor one side over the others. The mother of one of my customers owned an antique store for most of her life. She has numerous collections. After her mother passed, she gave me some of her mother's belongings. One of them is a large glass jar full of dice (about a gallon). At a glance, they all seem to have divots drilled out for the dots. The side with one dot retains most of the material in that side. The opposing side has six divots. More material has been removed from that side, than any other side. This means that the heaviest side of the die is opposite of the lightest side of the die. It would stand to reason that sixes would come up more often than ones. It would also stand to reason that straight sixes would come up more often than any other sequence.

Perhaps your wife is correct when it comes to the REAL world.

Now, lets apply this principle to a particle suspended in liquid. Based on it's imperfect shape, it would stand to reason that it would favor a motion in one direction, over all others.

OK. Fine. Suppose we have a hypothetical collection of dice such that each pip is painted on and each side is guaranteed to have the same amount of paint. (I.e., the side with 1 pip has it's pip painted with six times as much paint as a pip on the the side with 6).

Also, these dice are such that the center of mass of the paint is the same on each side and is evenly distributed about that center.

Are we done now?

 

[FrumiousBandersnatch]

As the illustration in the article you linked showed, the Na+ and Cl- ions gather clusters of water molecules, but don't fully bond to them.

Water itself also "autoionizes" (don't know if that's the word, I haven't taken chemistry in 30 years) with a fraction of water molecule pairs becoming OH- and H3O+ ions (again with neutral water clusters around them oriented by the charge). The pH of 7 for pure water represents the level of that autoionization. (1 part in 10^7 I think)

Thanks; I probably knew that at one time, briefly - it's been over 40 years for me, and I wasn't very keen on it at the time...

 

[HARK!]

OK. Fine. Suppose we have a hypothetical collection of dice such that each pip is painted on and each side is guaranteed to have the same amount of paint. (I.e., the side with 1 pip has it's pip painted with six times as much paint as a pip on the the side with 6).

Also, these dice are such that the center of mass of the paint is the same on each side and is evenly distributed about that center.

Are we done now?

Did I say that no die is perfectly weighted?

However, in the REAL world, no die is perfectly weighted.

Yes, yes I did.

You can't tell me that there is a perfect cube that has an equal number of molecules on every plane. Let alone adding paint to them, to keep track of which plane is which. Unless the die is perfectly balanced, down to the atomic level; it will favor landing on one side over another.

I hope that we are now done with this chapter of the discussion.

 

[Bradskii]

Now, lets apply this principle to a particle suspended in liquid. Based on it's imperfect shape, it would stand to reason that it would favor a motion in one direction, over all others.

Never playing dice with you...

And if a particle favours one motion out of all the others, a straight line might be it.

 

[HARK!]

And if a particle favours one motion out of all the others, a straight line might be it.

I would tend to agree; but then again an arc would seem more likely.