Astronomers should be sued for false advertizing. (2)

[Loudmouth]

Right. I have to jump through a ton of hoops based on limited information, but you can't even so much a site a single source of 'dark' stuff, and somehow that's "ok" by you? I'm supposed to simply *ignore* the fact that SUSY theory died a horrible agonizing death at the LHC?

You have to support your claims. Your claim is that photons will necessarily be absorbed by electrons in the intergalactic plasma. In order to support that claim you need to show us the measured density of plasma in intergalactic space, and demonstrate that what you claim occurs can occur.

 

[Michael]

I do embrace them. However, it is correct to say that photons have no kinetic energy in classical physics. They do in SR/GR. That is all that is being said.

No, that's *NOT* what he said. He *actually* said the following, and it's *not* a comparison between the mass concepts of "classical' physics and GR:

http://www.christianforums.com/t7688433-41/#post61575350

Photon "kinetic energy" cannot change (is always zero) and so has nothing to do with frequencey shifts.

Utterly false.

And there is that "kinetic" again. A photon always has a kineteic energy of zero .

Utterly false.

Not once did he say a word about the difference between GR and "classical physics.". He made *highly erroneous* statements. He's incapable of admitting making a mistake, so now you two are just making up excuses for both of your irrational (and false) claims.

I fully agree that Relativity is the accurate description of physics.

Then stop claiming photons have no mass! E=MC^2. M=E/C^2. Photons all have energy = Hf. M=Hf/C^2!

I am not arguing with you on that point. What is being clarified is that photons do not have mass in CLASSICAL physics, WHICH IS TRUE.

He didn't say *squat* about 'classical' physics in his original post. He just made false statements which I caught and he's been backpeddling ever since.

To this day, neither of you two has yet admitted that electrical discharges *do* occur in plasmas and solar flares!

I might as well be trying to teach QM to my cat.

 

[Loudmouth]

No, that's *NOT* what he said. He *actually* said the following, and it's *not* a comparison between the mass concepts of "classical' physics and GR:

This is what RC said in a very recent post:

"

• Photons have no classical kinetic energy and
• they do have relativistic kinetic energy

"

Notice the highlighted stuff in red.

Then stop claiming photons have no mass! E=MC^2. M=E/C^2. Photons all have energy = Hf. M=Hf/C^2!

As soon as you agree that photons do not have mass in classical physics, nor can they have kinetic energy in classical physics.

 

[Michael]

This is what RC said in a very recent post:

"

• Photons have no classical kinetic energy and
• they do have relativistic kinetic energy

"

Notice the highlighted stuff in red.

A "rational" person would have simply admitted that his two erroneous statements were in error and moved on. Instead he made up lame rationalizations as to why he was 'right' when he was actually as *wrong* as is humanly possible to be wrong on that topic! He didn't say *squat* about "classical" physics until *after* he got caught making false statements. He then tried to use that lame post to claim he "was right" all along! What a load of pure nonsense.

Do electrical discharges occur in solar flares LM?

As soon as you agree that photons do not have mass in classical physics, nor can they have kinetic energy in classical physics.

Apparently when you two use the term "classical physics' you really mean 'ignorant understanding of ancient physics that has nothing to do with modern cosmology theories or photon redshift".

 

[Loudmouth]

A "rational" person would have simply admitted that his two erroneous statements were in error and moved on. Instead he made up lame rationalizations as to why he was 'right' when he was actually as *wrong* as is humanly possible to be wrong on that topic! He didn't say *squat* about "classical" physics until *after* he got caught making false statements. He then tried to use that lame post to claim he "was right" all along! What a load of pure nonsense.

RC failed to specify that he was referring to classical physics, but he quickly indicated that he was. I understood exactly what he was talking about from the start. He is really talking about the differences between classical physics where photons and electrons collide like bowling balls and the real way in which they react which is not like bowling balls.

Why is this important? Because you were insisting on a bowling ball (i.e. classical physics) style interaction for photons and electrons. That's not how it works. When a photon loses momentum it HAS TO CHANGE TRAJECTORY. That is the point being made. You were trying to claim that some of the interactions did not result in a change of trajectory alluding to a bowling ball style of interacter per classical physics. This all ties back to Ned Wright's correct statement than any process that reduces the momentum of a photon must necessarily change its trajectory.

Do electrical discharges occur in solar flares LM?

I really haven't followed it that closely. I do get a kick out of your solid iron surface in the Sun. That is good for some laughs.

Apparently when you two use the term "classical physics' you really mean 'ignorant understanding of ancient physics that has nothing to do with modern cosmology theories or photon redshift".

Perhaps you should think about that for a bit, and then come back and tell us how an interaction between an electron and a photon can reduce the momentum of the photon without changing its trajectory.

 

[Michael]

RC failed to specify that he was referring to classical physics, but he quickly indicated that he was. I understood exactly what he was talking about from the start.

You made the same mistake he did! You claimed they had *no* mass, resting or otherwise as I recall. Neither of you seems to care to embrace SR, let alone GR. Apparently you intend to spend the rest of your lives arguing ancient physics trivia.

He is really talking about the differences between classical physics where photons and electrons collide like bowling balls and the real way in which they react which is not like bowling balls.

He made *two erroneous statements*! Both of them are *directly* related to the photon redshift issue! Both were false statements. He didn't say "squat" about "classical" anything until his show got busted!

Why is this important?

Because his statements are factually incorrect!

Because you were insisting on a bowling ball (i.e. classical physics) style interaction for photons and electrons. That's not how it works.

Yes, that is how it works! We have moving particles slamming into other relatively stationary particles.

When a photon loses momentum it HAS TO CHANGE TRAJECTORY.

Boloney! If you've ever played billiards/pool, the white ball sometimes loses it's momentum in a *forward* direction without being deflected. Sure, usually it is deflected, but *not every time*. It all depends on the *type* of scattering being discussed, and the *specific* angle of interaction. It's actually pretty easy to "scratch" by not putting any spin on the white cue ball and having it follow the ball it hit, and lost momentum to, right into the pocket!

That is the point being made. You were trying to claim that some of the interactions did not result in a change of trajectory alluding to a bowling ball style of interacter per classical physics.

I'm simply exploring *all* the options, *all* of the scattering types, and *all* of the interactions.

I really haven't followed it that closely. I do get a kick out of your solid iron surface in the Sun. That is good for some laughs.

Why can't you answer a simple yes or no question?

Perhaps you should think about that for a bit, and then come back and tell us how an interaction between an electron and a photon can reduce the momentum of the photon without changing its trajectory.

That's easy. It simply "hits" the electron "head on" and transfers momentum in the *same direction of travel*. A typical absorption/emission process effectively does the same thing.

 

[Loudmouth]

You made the same mistake he did! You claimed they had *no* mass, resting or otherwise as I recall. Neither of you seems to care to embrace SR, let alone GR. Apparently you intend to spend the rest of your lives arguing ancient physics trivia.

If you embraced SR and GR, you would understand that Ned Wright is correct when he states:

"There is no known interaction that can degrade a photon's energy without also changing its momentum, which leads to a blurring of distant objects which is not observed."

Yes, that is how it work. You have moving particle slamming into other relatively stationary particles.

So you reject GR and SR which require the photon to change trajectory if it loses momentum.

In the case of the head on collision for the billiard balls, one of the balls loses speed. This can't happen for photons. They are always moving at the speed of light.

Boloney! If you've every played billiards/pool, the white ball loses it's momentum in a *forward* direction without being deflected. It all depends on the *type* of scattering being discussed, and the *specific* angle of interaction.

That's not how it works. You are using classical physics instead of GR and SR.

Why can't you answer a simple yes or no question?

Because I don't know enough about the topic, but I do know enough about iron to know that you can't have a solid iron surface in the Sun.

That's easy. It simply "hits" the electron "head on" and transfers momentum in the *same direction of travel*. A typical absorption/emission process effectively does the same thing.

Plug in a zero theta into the equation for Compton scattering:

What is the change in wavelength with a theta of zero?

 

[Michael]

If you embraced SR and GR, you would understand that Ned Wright is correct when he states:

False dichotomy fallacy! Inelastic scattering has nothing to do with gravity.

"There is no known interaction that can degrade a photon's energy without also changing its momentum, which leads to a blurring of distant objects which is not observed."

Again, a lost of momentum isn't *automatically* a cause of 'blurring'. Ned makes no distinction between a loss of momentum and a change in direction. It's like claiming it's impossible to scratch in pool when hitting another ball into a pocket.

So you reject GR and SR which require the photon to change trajectory if it loses momentum.

Pfft. Your augments are based on ridiculous fallacies. GR has nothing to do with Compton scattering, or Brillioun scattering or any other type of inelastic scattering method. You're just 'making up" connections that do not even exist!

In the case of the head on collision for the billiard balls, one of the balls loses speed. This can't happen for photons. They are always moving at the speed of light.

They can and do lose momentum in *any* inelastic scattering process, including *head on* inelastic scattering events.

That's not how it works. You are using classical physics instead of GR and SR.

It is how it work, and it's not related to gravity theory, not 'classical Newtonian gravity theory, or Einsteins GR! You're handwaving away based on pure non-sequitor fallacies!

Because I don't know enough about the topic, but I do know enough about iron to know that you can't have a solid iron surface in the Sun.

I handed you folks 7 published papers that all claimed solar flares were associated with "electrical discharges', starting with Dungey. How is that a "tough" question even?

Plug in a zero theta into the equation for Compton scattering:

Why? It's only *one* kind of scattering!

 

[Loudmouth]

Again, a lost of momentum isn't *automatically* a cause of 'blurring'.

Lost momentum results in a change in trajectory, so yes, it does cause blurring.

Ned makes no distinction between a loss of momentum and a change in direction.

The loss in momentum is what causes the change in direction. They are one in the same.

Pfft. Your augments are based on ridiculous fallacies. GR has nothing to do with Compton scattering, or Brillioun scattering or any other type of inelastic scattering method. You're just 'making up" connections that do not even exist!

According to relativity, photons are always travelling at c, correct?

So what is the speed of the photon after it collides with an electron?

I handed you folks 7 published papers that all claimed solar flares were associated with "electrical discharges', starting with Dungey. How is that a "tough" question even?

So says the guy who thinks that there is a solid iron surface in the Sun.

Why? It's only *one* kind of scattering!

You can't do the math?

 

[Michael]

Lost momentum results in a change in trajectory, so yes, it does cause blurring.

And there is indeed blurring, particularly the most redshifted objects.

The loss in momentum is what causes the change in direction. They are one in the same.

No, they are not. That billiard ball example demonstrates that they are not one and the same.

According to relativity, photons are always travelling at c, correct?

Yes, but they can gain and lose momentum, and become blueshifted and redshifted as a result.

So what is the speed of the photon after it collides with an electron?

Same speed, different wavelength.

So says the guy who thinks that there is a solid iron surface in the Sun.

Pure dodge. You two have no interest in resolving anything.

You can't do the math?

Why should I limit myself to a *single* kind of inelastic scattering in the first place?

 

[Loudmouth]

Yes, but they can gain and lose momentum, and become blueshifted and redshifted as a result.

In order to lose momentum, they have to leave at a different trajectory.

Same speed, different wavelength.

And different trajectory.

Pure dodge. You two have no interest in resolving anything.

Perhaps we could resolve the melting point of Iron. Do you know what it is?

We could also go over the zeroeth law of thermodynamics. Do you understand that law?

Why should I limit myself to a *single* kind of inelastic scattering in the first place?

They all do the same thing, Michael. The change in momentum requires a change in trajectory.

You also have not shown that intergalactic plasma is even dense enough to interact with all of the photons passing through it. If there is enough plasma to redshift all of the photons from the nearest galaxies then you have a very serious problem because now we will have a plasma too dense to see distant galaxies as Elendur has discussed.

Plasmas are not transparent. They scatter light, and they do so in those oh so precious lab experiments that you go gaga over.

 

[Elendur]

Michael, I think you missed my post again (though I might've missed your response, in that case I'd like a link)
Link to post:
#212

 

[Michael]

Michael, I think you missed my post again (though I might've missed your response, in that case I'd like a link)
Link to post:
#212

Thanks. I haven't forgotten you, but has been a busy couple of weeks. Hopefully today I'll have some time to invest in researching a bit more about the various scattering methods.

It seems to me that the entire debate comes down to two basic claims:

In order to lose momentum, they have to leave at a different trajectory.

While this is (may be?) true of some types of scattering, it's not necessarily the case in *all* kinds of scattering. This is the first claim that warrants scrutiny IMO.

Could you explain to me then, what is the controlling mechanism that returns the photons on course?

This is really the only other relevant issue IMO. While some photons will certainly never reach Earth, other photon can and do "bounce around" a bit and still reach us at Earth, albeit with some "blur", particularly at the greatest redshifts.

I'm *finally* catching up on Earth. Bear with me a bit, but I will tackle your post shortly.

 

[Michael]

In order to lose momentum, they have to leave at a different trajectory.

How do you *know* that is true for *all* types of inelastic scattering processes?

Perhaps we could resolve the melting point of Iron. Do you know what it is?

That conversation is really better suited for the appropriate thread on Electric sun theory. Technically speaking the "crust" is composed of many elements, and the melting point of Carbon is around 4000K as I recall.

Just as the photosphere is cooler and thicker than the chromosphere, and the chromosphere is cooler and thicker than the corona, the plasma double layers under the photosphere are cooler and thicker than the predominantly Neon photosphere.

We could also go over the zeroeth law of thermodynamics. Do you understand that law?

The laws of thermodynamics do not prevent the chromosphere from being hotter and thinner than the photosphere. Likewise, the laws of thermodynamics allow for thicker, cooler layers to exist in the solar atmosphere.

They all do the same thing, Michael. The change in momentum requires a change in trajectory.

That's a rather "bold" and currently unsupported statement. How about demonstrating that point, inelastic scattering method by inelastic scattering method.

You also have not shown that intergalactic plasma is even dense enough to interact with all of the photons passing through it.

You haven't shown it to be "thin enough" to pass through it unabated! In fact we just discovered the universe is more "dusty" than we imagined, and the closest galaxies are at least twice as bright as astronomers "predicted".

If there is enough plasma to redshift all of the photons from the nearest galaxies then you have a very serious problem because now we will have a plasma too dense to see distant galaxies as Elendur has discussed.

A lot depends on *exactly* which inelastic scattering method is most responsible for the redshift. I can't answer that question yet, but I'm looking into it.

Plasmas are not transparent. They scatter light, and they do so in those oh so precious lab experiments that you go gaga over.

Ya, and they do so in space, particularly in certain directions and wavelengths where the universe is most dusty and most "opaque". It really depends on which direction we are discussing an which wavelength we're talking about.

 

[Elendur]

Thanks. I haven't forgotten you, but has been a busy couple of weeks. Hopefully today I'll have some time to invest in researching a bit more about the various scattering methods.

It seems to me that the entire debate comes down to two basic claims:

I'll go along with it, not entirely content though (since it'll probably result in some additional backtracking in order to find where we might differ).

While this is (may be?) true of some types of scattering, it's not necessarily the case in *all* kinds of scattering. This is the first claim that warrants scrutiny IMO.

The phenomena called "scattering" has its definition. That definition requires a change in trajectory in order to call it scattering.
I've chosen to address the inelastic scatterings since they seem to be the ones that could have the potential to explain the observed redshift.

This is really the only other relevant issue IMO. While some photons will certainly never reach Earth, other photon can and do "bounce around" a bit and still reach us at Earth, albeit with some "blur", particularly at the greatest redshifts.

Great, if you're able to answer that question we'll be able to work from that. If you cannot, we'll have to backtrack some, but I believe that it'll be worth it.

I'm *finally* catching up on Earth. Bear with me a bit, but I will tackle your post shortly.

 

[RealityCheck01]

That conversation is really better suited for the appropriate thread on Electric sun theory. Technically speaking the "crust" is composed of many elements, and the melting point of Carbon is around 4000K as I recall.

Technically speaking that "crust" has a composition that depends on the phase of the Moon and what side of the bed you got up on. But your web site is very clear. The fantasy is that there is a solid iron ferrite surface in the Sun somewhere under the photosphere that ignorance about the Sun has lead you to think can be seen in images. The major ignorance is that you have no idea what photosphere means. It is where light is emitted from within the Sun so any plasma that emits light in the body of the Sun is inside the photosphere!

The temperature of the Sun's core is ~13,000,000 K.
The temperature of the photosphere is ~5700 K.
There is a temperature gradient from the core to the surface of ~13,000,000 K to ~5700 K. Iron has a melting point of 1811 K. Thus your crust does not exist.
In fact the temperature of the photosphere is ~9400 K at at depth of ~100 km.

As stated in the appropriate thread on Electric sun theory: Michael's iron surface idea completely debunked!

Any one with high school physics (second law of thermodynamics + temperature of the Sun) can see that Michael 's iron surface idea is a fantasy:
8th July 2009: Your hypothetical solid iron surface has been in thermal contact with at least one object that has consistently had a temperature large enough to vaporize iron for about 4.57 billion years.
17th April 2010: Why this iron crust thermodynamically impossible
17th April 2010: Iron Sun Surface Thermodynamically Impossible IV

Just as the photosphere is cooler and thicker than the chromosphere, and the chromosphere is cooler and thicker than the corona, the plasma double layers under the photosphere are cooler and thicker than the predominantly Neon photosphere.

Once again your ignorance of solar physics is showing !
The photosphere is predominantly H and He (98% by mass) with traces of other elements such as O, C, Fe, Ne, N, Si, etc. Errors in Michael's site II (photosphere is not Ne and Si)!

There are no "plasma double layers under the photosphere" (or even single layers) because convection mixes the plasma up: Errors in Michael's site XXV: gooey, insulating Si and crusty Ca layers do not exist!

The body of the Sun is different from the atmosphere as has been explained to you many times at the JREF forum:
17th April 2010: I've explained to you MANY times why you're totally wrong about this. ...
This boils down to the simple fact that the photosphere is different from the corona! So no one should expect them to act exactly the same.

The laws of thermodynamics do not allow for thicker, cooler layers to exist in the solar body. An analogy may help - does anyone here expect there to be a layer of ice in a pot of boiling water? That is what you expect to happen, Michael .

 

[Loudmouth]

While this is (may be?) true of some types of scattering, it's not necessarily the case in *all* kinds of scattering. This is the first claim that warrants scrutiny IMO.

Then show us this scattering process that doesn't scatter light, and show how the intergalactic plasma is able to produce this scattering as well as the requisite redshift through this mechanism.

While some photons will certainly never reach Earth, other photon can and do "bounce around" a bit and still reach us at Earth, albeit with some "blur", particularly at the greatest redshifts.

And some will not interact with the plasma at all, producing the spectral band where we expect it, as RC's math demonstrated. It is until you to galaxies 10 billion light years away that you get significant interaction for all photons.

Also, you have not shown what percentage of photons would reach Earth. That is a very important number that you need to calculate.

 

[RealityCheck01]

It looks like you, Michael, have no probelm following the math or physics in this post since you have not answered.

My calculations are really simple. But since you did not understand them, here in one is in baby steps:
Michael: Tired light theories predict no detectable redshift through scattering!
The defintion of mean free path gives that the transmission is


where l is the mean free path !

1. Mean free path of a photon in the ICM is ~10 billion years.
2. A 'slab' of the ICM between us and a galaxy x light years away will have the above transmission.
3. A galaxy 10 billion light years away has a transmission of its intensity times 1/e so 37% of the photons do not scatter.
4. We can detect light from galaxies that are further than 10 billion light years away.
5. Thus we will see non-red-shifted spectral lines in galaxies up 10 billion light years away at least.

Any problem with following the math or physics, Michael?

That this rules out scattering as cosmological redshift is obvious.
Michael: Scattering blurs distant galaxies compared to near galaxies! is equally obvious.

There are Michael's seven non-cosmological "redshift"s that show up in the lab but all of the scattering ones are ruled out, e.g.
Compton scattering = cosmological redshift will blue-shift visible lght!
and the other ones need specific conditions that do not exist in the intergalactic medium.

Thus we can stop talking about processes that scatter photons from plasma and change their wavelength and look for processes that do not scatter photons but still change their wavelength.
I will start the list. You can add to it Michael:

1. An expanding universe.
2. Michael?

P.S. Outstanding questions for you, Michael
Michael, can you provide evidence peer-reviewed scientific literature that the following can cause cosmological redshift?
First asked 14th November 2012

What effect does the "double brightness" paper have on the % of normal matter?
First asked 18 November 2012.

 

[davidbilby]

How do you *know* that is true for *all* types of inelastic scattering processes?

Of all the inelastic scattering processes known, can you show a single example where a change in wavelength can occur with θ = 0?

HINT: Billiard balls are far from a good example of how quantum mechanics works, maybe used in high school (not even that really, but whatever)...

That's a rather "bold" and currently unsupported statement. How about demonstrating that point, inelastic scattering method by inelastic scattering method.

It's currently an entirely supported statement.

Elendur isn't quite right in one detail, strictly speaking - it is perfectly acceptable to have a "scattering" angle of zero as regards scattering mathematics, irrespective of the semantics of the word, but if you take Compton scattering as an example, as has been pointed out repeatedly....the zero value of theta requires that the difference in wavelength before and after is zero.

The travel distance for a photon from a distant galaxy to us means that a scattering angle of anything other than zero (or so imperceptibly close to zero as makes no difference) would result in that photon "missing" its target.

Given the multiple (millions?) of scattering interactions you seem to be assuming happening en route and then averaging out...the chance of numerous non-zero angles adding up bang on to zero in a three dimensional space on a routine and consistent basis...is incalculably large.

Compton scattering is ruled out for other reasons too, particularly the fact that the temperatures involved would cause subsequent blueshifts due to the thermal motion of the scattered electrons. This was pointed out by Higgs (L.A., not Peter) based on work by Paul Dirac, which also noted that the width of Compton-scattered lines was simply too great to be part of the observed cosmological redshift. Not to mention a further failure, namely that Compton scattering is strongly wavelenth dependent where the cosmological redshift is observed to be strongly wavelength independent.

A lot depends on *exactly* which inelastic scattering method is most responsible for the redshift. I can't answer that question yet, but I'm looking into it.

That's nice, since you've previously said it as a statement of fact that "The causes of plasma redshift include Compton redshift, the Wolf effect, Stark redshift and what Chen et all called 'plasma redshift". Still so sure about that?

The Wolf effect, AC Stark effect (as in Chen's paper, it's simply that) are wavelength dependent - which rules them out right away. Not to mention that both consistently create redshifts AND blueshifts, so there should logically be blueshifted quasars (spotted any?).

Also, the Wolf effect you're citing only applies to correlated non-Lambertian sources, and cannot produce line shifts greater than the width of the spectral line - unless you are considering it in tandem with Brillouin scattering...which of course would be somewhat ridiculous on the cosmological scale unless you wish to claim some kind of geocentric universal correlation of the intergalactic medium respective to us here on Earth, as well as the correlation of the many photons heading in our direction such that the Wolf effect could be observed in the first place...

So...it really doesn't depend on which one is 'most responsible' though, because you haven't shown that *any* inelastic scattering can lead to the observed cosmological redshift (strongly wavelength and specially independent, essentially consistent over time and in every direction we look).

Before saying which one is 'most responsible' perhaps you should try and show that any of them 'can be responsible' at all....

 

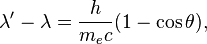
[Michael]

Of all the inelastic scattering processes known, can you show a single example where a change in wavelength can occur with θ = 0?

Not really, at least not yet. Brillouin scattering looks promising to me for a variety of reasons, but I seem to have a lot of research to do to really get much of a handle on the various scattering options.

Most of your criticisms related to a pure Compton scattering process have some merit, save this particular comment:

Before saying which one is 'most responsible' perhaps you should try and show that any of them 'can be responsible' at all....

I think the onus of responsibility is on you to demonstrate that none of them have *any* influence on photons in space. That is essentially your claim.

It's *not* true that distance galaxies are perfectly clear. They are in fact "blurred".

It's *not* true that *no* Compton scattering occurs in space.

The effects of plasma and dust on light has been demonstrated in the lab. The results from the lab have already demonstrated that all of them *can* be responsible for photon redshift.

What has *never* been shown is that "dark energy" A) exists at all, or B) has any tangible effect on a photon. In other words *you* have never met your own requirement related to your use of the word "can". Compton redshift *can* cause photons to experience redshift as demonstrated in the lab. You cannot even name a source of "dark energy' let alone show it 'can" do anything to a photon.

At least I'm willing to admit I have work to do, whereas you seem to ignore your responsibilities entirely IMO.